【中2数学】（2020年12月）学習進度。

第１週（㉒ 証明）

・問題

　$y = x$上の点$\mathrm{A}$から$x$軸、$y$軸へひいた垂線と軸との交点をそれぞれ$\mathrm{B}, \mathrm{C}$とする。
$\triangle \mathrm{OAB} \equiv \triangle \mathrm{OAC}$であることを証明しなさい。

・解答例

　点$\mathrm{A}$は$y = x$上にあるので、$\angle \mathrm{AOB} = 45^\circ$
$\angle \mathrm{AOC} = 90^\circ - \angle \mathrm{AOB}$
　$= 90^\circ - 45^\circ = 45^\circ$
よって、$\angle \mathrm{AOB} = \angle \mathrm{AOC}$（①）

$\angle \mathrm{OAB} = 180^\circ - 90^\circ - \angle \mathrm{AOB}$
　$= 90^\circ - 45^\circ = 45^\circ$
$\angle \mathrm{OAC} = 180^\circ - 90^\circ - \angle \mathrm{AOC}$
　$= 90^\circ - 45^\circ = 45^\circ$
よって、$\angle \mathrm{OAB} = \angle \mathrm{OAC}$（②）

$\mathrm{OA}$は共通（③）

①、②、③より、１組の辺とその両端の角が等しいから、
$\triangle \mathrm{OAB} \equiv \triangle \mathrm{OAC}$

第２週（㉓ 二等辺三角形）

・問題

　点$\mathrm{A}, \mathrm{B}$をそれぞれ中心として、等しい半径の円をかき、その２円の交点を通る直線をひいた。この直線が、線分$\mathrm{AB}$の垂直二等分線であることを証明しなさい。

・解答例

　仮定より、$\mathrm{AP} = \mathrm{BP}$で$\triangle \mathrm{ABP}$は二等辺三角形であるから、
$\angle \mathrm{BAP} = \angle \mathrm{ABP}$（①）

また、$\mathrm{AP} = \mathrm{BP}, \mathrm{AQ} = \mathrm{BQ}, \mathrm{PQ}$は共通であり、３組の辺が、それぞれ等しいから、
$\triangle \mathrm{APQ} \equiv \triangle \mathrm{BPQ}$
よって、$\angle \mathrm{APQ} = \angle \mathrm{BPQ}$（②）

　①より$\angle \mathrm{OAP} = \angle \mathrm{OBP}$、②より$\angle \mathrm{APO} = \angle \mathrm{BPO}$、仮定より$\mathrm{AP} = \mathrm{BP}$であり、１組の辺とその両端の角が、それぞれ等しいから、
$\triangle \mathrm{AOP} \equiv \triangle \mathrm{BOP}$

　よって、$\mathrm{AO} = \mathrm{BO}$
$\angle \mathrm{AOP} = \angle \mathrm{BOP}$で、その角度は$\dfrac{180^\circ}{2} = 90^\circ$
ゆえに、直線$\mathrm{PQ}$は、線分$\mathrm{AB}$の垂直二等分線である。

第３週（㉒ 証明）

・問題

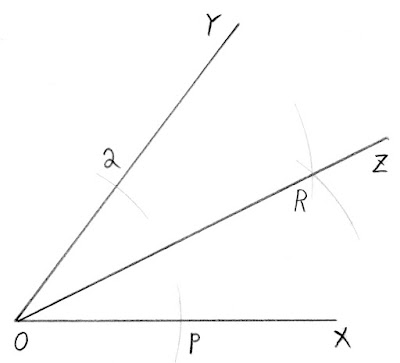
　点$\mathrm{O}$を中心とする円をかき、半直線$\mathrm{OX}, \mathrm{OY}$との交点を、それぞれ$\mathrm{P}, \mathrm{Q}$とする。２点$\mathrm{P}, \mathrm{Q}$を、それぞれ中心として、等しい半径の円をかく。その交点の１つを$\mathrm{R}$とし、半直線$\mathrm{OZ}$をひく。

半直線$\mathrm{OZ}$が、$\angle \mathrm{XOY}$の二等分線であることを証明しなさい。

・解答例

　仮定より、$\mathrm{OP} = \mathrm{OQ}, \mathrm{PR} = \mathrm{QR}$
$\mathrm{OR}$は共通であり、３組の辺が、それぞれ等しいから、
$\triangle \mathrm{OPR} \equiv \triangle \mathrm{OQR}$

よって、$\angle \mathrm{POR} = \angle \mathrm{QOR}$
ゆえに、$\angle \mathrm{XOZ} = \angle \mathrm{YOZ}$であり、半直線$\mathrm{OZ}$は、$\angle \mathrm{XOY}$の二等分線である。

第４週（㉓ 二等辺三角形）

・問題

　二等辺三角形の頂角の二等分線は、底辺を垂直に２等分する。これを証明しなさい。

・解答例

　二等辺三角形$\mathrm{ABC}$の$\mathrm{AB} = \mathrm{AC}, \angle \mathrm{ABC} = \angle \mathrm{ACB}$とする。
$\angle \mathrm{BAC}$の二等分線と$\mathrm{BC}$との交点を$\mathrm{H}$とおくと、
$\angle \mathrm{BAH} = \angle \mathrm{CAH}, \mathrm{AB} = \mathrm{AC}, \mathrm{AH}$は共通であり、
２組の辺とその間の角が、それぞれ等しいから、
$\triangle \mathrm{ABH} \equiv \triangle \mathrm{ACH}$
よって、$\angle \mathrm{AHB} = \angle \mathrm{AHC}$であり、その角度は$\dfrac{180^\circ}{2} = 90^\circ$、
$\mathrm{BH} = \mathrm{CH}$、ゆえに、二等辺三角形$\mathrm{ABC}$の頂角の二等分線$\mathrm{AH}$は、底辺$\mathrm{BC}$を垂直に２等分する。