共通テスト数学II・Bの第１問に触発されて、三角関数の合成について再考してみた。

１　三角関数の合成

　Twitterで「共通テスト数学II・Bを解いてみる。第１問はシンプルだけど案外奥が深い良問だと思った。三角関数の合成について、その本質をきちんと理解しているかどうか、暗に問うている問題だなぁ。そこまで突き詰めなくても、何となく解けてしまうけれど・・・」とツイートした。
このツイートの趣旨を説明することは、現在あるいはこれから三角関数の合成の基礎を学習する高校生、将来の受験生にとって有益だと思うので記事にすることにした。

２　三角関数のグラフ

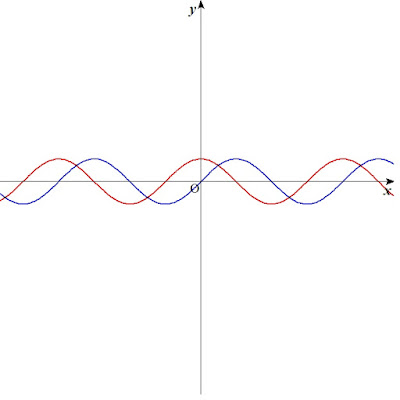
　まず三角関数のグラフを思い出してもらいたい。
次の図は、サインカーブとコサインカーブ（正弦曲線・余弦曲線）のグラフである。

問題の関数は$y = \sin \theta + p \cos \theta$である。
$p = 1$のとき$\sin \theta + \cos \theta$になるので、まずそのグラフの形を見てみよう。

三角関数の$\theta$に何かを足したりかけたり、あるいは三角関数自体に何かを足したりかけたり、いろいろな三角関数同士あるいは三角関数とは別種の関数を合成したりして、いろいろな波形、波動をつくることができる。
いろいろな波形を合成したり分離したりする信号処理の手法は、数学だけでなく、と言うより数学以外の分野で広く活用されている。
電気工学や電子工学などの工学はもちろん、物理学を含む理学全般で活用されていると言ってもよいだろう。

３　問題の捉え方の例示

　今回の問題の解答を考察してみたい。
$0 \leq \theta \leq \dfrac{\pi}{2}$の範囲で考えないといけない。
$p = 0$のとき、この関数は単純なサインカーブとなる。

　$p > 0$のときは次の図のようなグラフ（$p = 3$で作成）になるけれど、最大値とそのときの$\theta$の値を計算するには、まさに教科書で学習する三角関数の基礎、三角関数の合成公式を活用することができる。

４　マイナスをかけると逆になる

　マイナスをかけると上下（$y$）あるいは左右（$x$）逆になる。
三角関数でも同様である。
そのことに注意して、$p < 0$のときのグラフ（$p = -3$で作成）を見てほしい。

$0 \leq \theta \leq \dfrac{\pi}{2}$の範囲では、$\theta = \dfrac{\pi}{2}$のときこの関数は最大になる。

このことは$\sin x$、$p \cos x$、その合成関数のグラフの形から明らかである。

　教科書で学習した三角関数に関する公式についての知識だけでなく、三角関数とその合成についての本質的な理解を問うているという意味で、この問題自体は良問だと思う。
ただ、適当な直感でも解けてしまうので、共通テストの問題として妥当どうかは、まだよく分からない。