インピーダンス

　今回は、インピーダンスの話です。

インピーダンス$Z = \dfrac{V}{I}$

電圧と電流の比であり、分数である。
分数は比であり、比は分数として表現できる。
電気の法則、オームの法則はV = RIでしたね。

抵抗$R = \dfrac{V}{I}$

また、リアクタンス$X = \dfrac{V}{I}$

$\dfrac{V}{I}$を抵抗と言ったり、リアクタンスと言ったり、インピーダンスと言ったり・・・一体どういうことなのか？

　結局、電気の話はつまるところ、電圧と電流の比に帰着する。
これが本質なのではないでしょうか？
電気の世界は、電気を通す銅線等の導体の中を、電気が流れる。
回路に電圧がかかって、電流が流れる。
その回路に、抵抗があったり、リアクタンスがあったりする。
現実の世界の電気回路には、抵抗やコイルやコンデンサなど、いろいろな要素が複雑にからんでいる。

回路に抵抗しかなければ、直列だろうと並列だろうと、合成抵抗を計算すればよかった。
しかし、回路には抵抗だけでなく、コイルやコンデンサの要素もあるので、リアクタンスも考慮しないといけない。
現実の世界は複雑で、電池に豆電球つなげたら点いたみたいな、単純な話ではない。
電気は我々の生活を支えている訳ですから。

　対象となる電気回路におけるインピーダンスを考えるとは、要するに結局、電圧と電流の比を考えることである。
抵抗やコイルやコンデンサなど、いろいろな要素が複雑にからんでいる現実の世界の電気回路においても、電圧と電流の比、インピーダンスを計算することができる。
インピーダンスの計算は、抵抗だけしかない回路よりも複雑です。
直列であっても複雑で、並列だともっと難しい。

この講座では並列の場合は省略し、直列の場合だけ話します。
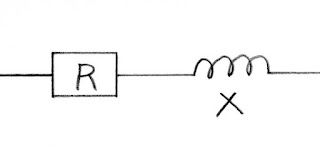
例えば、抵抗とコイルが直列につながっている場合。

直列の合成抵抗を計算するノリだと、R + Xと計算したくなりますよね。
違うんです、直列につながってるだけでも、そんな単純な計算にはならない。

$Z^2 = R^2 + X^2$

$Z = \sqrt{R^2 + X^2}$

　そして、いよいよピタゴラスの定理の話です。

直角三角形の斜辺がZで、他の２辺がRとXです。
位相のズレが90度だったという話ですね。
電気工事士の試験でしたら、ここまで勉強したらよいのではないでしょうか。

三相とかの話もありますが、この講座では省略します。
あれは、電源が３つあるので$3$という数字と、360 ÷ 3 = 120度ズレるので180 - 120 = 60度の三角比の中の$\sqrt{3}$という数字が計算に入ってきます。

・原案：Shall we インピーダンス?（オンライン補習塾 from 東三河）

・第二種電工数学入門講座に戻る。