ペンローズのグラフ記法。

１　ペンローズのグラフ記法

　下記のサイトで勉強したことをメモ。
・ペンローズのグラフ記法によるベクトル解析の公式の表現 低音（note）

・ペンローズのグラフ記法による完全反対称レビチビタテンソルの公式の表現 低音（note）

・ペンローズの論文

以下はウィキペディアの記事。
・ペンローズのグラフ記法、レヴィ＝チヴィタの記号、アインシュタインの縮約記法

２　スカラーとベクトル

（１）スカラー：$f$

（２）ベクトル：$\vec{u}$

（３）ベクトルの内積：$\vec{u} \cdot \vec{v} = u_i \delta_{ij} v_j$

（４）ベクトルの外積：$\vec{u} \times \vec{v} = \varepsilon_{ijk} u_j v_k$

３　レヴィ＝チヴィタの記号

（１）2階

$\varepsilon_{ij} = \left\{
\begin{array}{l}
1 \quad (i, j) = (1, 2)\\
-1 \quad (i, j) = (2, 1)\\
0 \quad i = j\\
\end{array}
\right.$

（２）3階

$\varepsilon_{ijk} = \left\{
\begin{array}{l}
1 \quad \text{偶置換}\\
-1 \quad \text{奇置換}\\
0 \quad \text{それ以外}\\
\end{array}
\right.$

（３）縮約公式

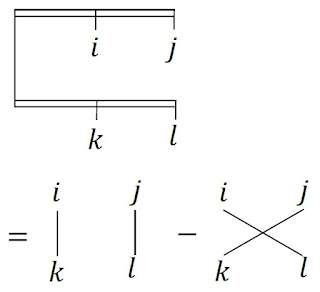
$\varepsilon_{ijm} \varepsilon_{klm} = \delta_{ik} \delta_{jl} - \delta_{il} \delta_{jk}$

４　内積・外積に関する公式

（１）スカラー3重積：$A \cdot (B \times C)$

（偶置換$1$、奇置換$-1$）

（２）ベクトル3重積：$A \times (B \times C) = B(A \cdot C) - C(A \cdot B)$

偶置換で次のように変換できる。

よって、

（３）ベクトル4重積：$(A \times B) \cdot (C \times D) = det\begin{pmatrix} A \cdot C & A \cdot D\\ B \cdot C & B \cdot D \end{pmatrix} = (A \cdot C)(B \cdot D) - (A \cdot D)(B \cdot C)$

よって、

５　テンソル

（１）テンソル$T_{k}^{ij}$

（２）クロネッカーのデルタ$\delta_{j}^{i}$

（３）レヴィ＝チヴィタ・テンソル

・$\varepsilon_{ij \cdots k}$

・$\varepsilon^{ij \cdots k}$

・$\varepsilon^{ij \cdots k} \varepsilon_{pq \cdots r}$

（４）軽量テンソル

・$g_{ij}$

・$g^{ij}$

（５）3次元：$\varepsilon^{ijk} \varepsilon_{pqr}$

・縮約公式（1）：$\varepsilon^{ijk} \varepsilon_{pqk} = \delta_{p}^{i} \delta_{q}^{j} - \delta_{q}^{i} \delta_{p}^{j} (= \varepsilon^{ij} \varepsilon_{pq})$

・縮約公式（2）：$\varepsilon^{ijk} \varepsilon_{pjk} = 2!\delta_{p}^{i} (= \varepsilon_{p}^{i})$

・縮約公式（3）：$\varepsilon^{ijk} \varepsilon_{ijk} = 3!$