二次方程式の係数が複素数の場合。
1 二次方程式の解の公式
中学や高校の数学で習う二次方程式の解の公式について、少し考察してみたい。実数$a, b, c$を係数とする二次方程式$ax^2 + bx + c = 0$の解は、
$x = \dfrac{-b \pm\sqrt{b^2 - 4ac}}{2a}$である。
高校数学の範囲では一般に、係数が実数の場合しか扱わない。
係数が虚数や複素数の場合、いろいろと面倒なことが生じ得るからである。
興味がある人はネットで調べて、詳しい解説を読んでみるとよいと思う。
・虚数係数2次方程式における解の公式/判別式/解と係数の関係の利用(受験の月)
・2次方程式の解のちょっとした小手技(数学のいずみ)
2 係数が複素数の場合
係数が複素数の二次方程式について、自分なりに考察してみた。以下、$a, b, c, d, e, f$は実数とする。
$(a + bi)x^2 + (c + di)x + (e + fi) = 0$
$(ax^2 + cx + e) + (bx^2 + dx + f)i = 0$
ここで、$A = at^2 + ct + e, B = bt^2 + dt + f$とおくと
$A = a\left( t^2 + \dfrac{c}{a}t \right) +e = a\left( t + \dfrac{c}{2a} \right)^2 - \dfrac{c^2}{4a^2} + e$
$A + \dfrac{c^2}{4a^2} - e = a\left( t + \dfrac{c}{2a} \right)^2$
$\dfrac{A + \dfrac{c^2}{4a^2} - e}{a} = \left( t + \dfrac{c}{2a} \right)^2$
$\pm\sqrt{\dfrac{A + \dfrac{c^2}{4a^2} - e}{a}} = t + \dfrac{c}{2a}$
$t = \pm\sqrt{\dfrac{A + \dfrac{c^2}{4a^2} - e}{a}} - \dfrac{c}{2a}$
これを$B = bt^2 + dt + f$に代入すると
$B = b\left( \pm\sqrt{\dfrac{A + \dfrac{c^2}{4a^2} - e}{a}} - \dfrac{c}{2a} \right)^2 + d\left( \pm\sqrt{\dfrac{A + \dfrac{c^2}{4a^2} - e}{a}} - \dfrac{c}{2a} \right) + f$
3 複素数平面上の軌跡
$A + Bi$の$A, B$を実数と仮定し、実部$A$、虚部$B$の複素数として複素数平面上にその軌跡を描くと上記の式となる。$X$軸を実軸、$Y$軸を虚軸とすると
$Y = b\left( \pm\sqrt{\dfrac{X + \dfrac{c^2}{4a^2} - e}{a}} - \dfrac{c}{2a} \right)^2 + d\left( \pm\sqrt{\dfrac{X + \dfrac{c^2}{4a^2} - e}{a}} - \dfrac{c}{2a} \right) + f$
このグラフが原点を通るなら、$A=0, B=0$となる場合があるので、実数解を有する可能性がある。
4 適当な具体例
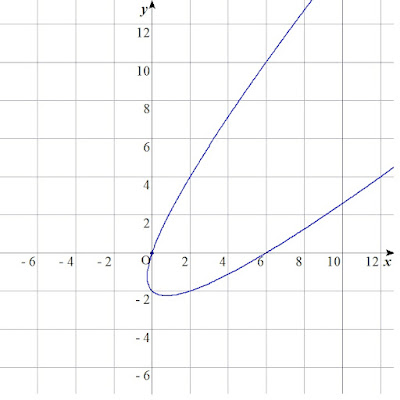
GRAPESで描画してみました。$a = 1, b = 1, c = 3, d = 5, e = 2, f = 4$のとき$(1 + i)x^2 + (3 + 5i)x + (2 + 4i) = 0$
$(x^2 + 3x + 2) + (x^2 + 5x + 4)i = 0$
$X = t^2 + 3t + 2, Y = t^2 + 5t + 4$とおくと
$Y = \left( \pm\sqrt{X + \dfrac{9}{4} - 2} - \dfrac{3}{2} \right)^2 + 5\left( \pm\sqrt{X + \dfrac{9}{4} - 2} - \dfrac{3}{2} \right) + 4$
$= \left( \pm\sqrt{X + \dfrac{1}{4}} - \dfrac{3}{2} \right)^2 + 5\left( \pm\sqrt{X + \dfrac{1}{4}} - \dfrac{3}{2} \right) + 4$
$= \left( X + \dfrac{1}{4} \right) \mp 3\sqrt{X + \dfrac{1}{4}} + \dfrac{9}{4} \pm 5\sqrt{X + \dfrac{1}{4}} - \dfrac{15}{2} + 4$
$= X \pm 2\sqrt{X + \dfrac{1}{4}} - 1$
・複素数と二次方程式・二次関数(まとめ記事)に戻る。