R元年度第2回高認物理基礎大問4解説
大問4
問1【周期】
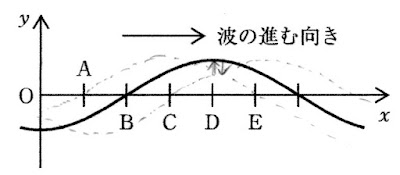
$x$軸の正の向きに進む正弦波がある。図のように、実線の状態から0.6s後に初めて破線の状態になった。
この正弦波の周期は何sか。
・0.6sで6m進んだので、正弦波の速さは$\dfrac{6}{0.6} = \dfrac{60}{6} = 10$(m/s)
また、正弦波の波長は8mなので、振動数$f = \dfrac{10}{8} = \dfrac{5}{4}$
よって、周期$T = \dfrac{1}{f} = \dfrac{1}{\dfrac{5}{4}} = \dfrac{4}{5} = 0.8$(s)
A~Eのうち、この時刻における媒質の速度が0である位置はどれか。
また、正弦波の波長は8mなので、振動数$f = \dfrac{10}{8} = \dfrac{5}{4}$
よって、周期$T = \dfrac{1}{f} = \dfrac{1}{\dfrac{5}{4}} = \dfrac{4}{5} = 0.8$(s)
問2【媒質の速度が0の点】
図は、$x$軸の正の向きに進む正弦波のある時刻における波形である。A~Eのうち、この時刻における媒質の速度が0である位置はどれか。
・D
それぞれ別々に鳴らすとおんさAの方がおんさBよりわずかに高い音を出し、同時に鳴らすと1sあたり3回のうなりが生じた。
次に、おんさAと振動数440Hzの標準おんさを、別々に鳴らすとおんさAの方が標準おんさよりわずかに高い音を出し、同時に鳴らすと1sあたり2回のうなりが生じた。
おんさAの振動数$f_{\mathrm{A}} \mathrm{[Hz]}$とおんさBの振動数$f_{\mathrm{B}} \mathrm{[Hz]}$を求めよ。
・$f_{\mathrm{A}} = 440 + 2 = 442$(Hz)
問3【うなりと振動数】
振動数が分からないおんさAとおんさBがある。それぞれ別々に鳴らすとおんさAの方がおんさBよりわずかに高い音を出し、同時に鳴らすと1sあたり3回のうなりが生じた。
次に、おんさAと振動数440Hzの標準おんさを、別々に鳴らすとおんさAの方が標準おんさよりわずかに高い音を出し、同時に鳴らすと1sあたり2回のうなりが生じた。
おんさAの振動数$f_{\mathrm{A}} \mathrm{[Hz]}$とおんさBの振動数$f_{\mathrm{B}} \mathrm{[Hz]}$を求めよ。
・$f_{\mathrm{A}} = 440 + 2 = 442$(Hz)
$f_{\mathrm{B}} = 442 - 3 = 439$(Hz)
【参考】
・うなり。:https://tanakah17191928.blogspot.com/2023/06/blog-post_18.html
スピーカーから出る音の振動数を$f_0$から徐々に大きくしていったところ、まず振動数$f_1$で共鳴し、次に振動数$f_2$で共鳴した。
$f_2$は$f_1$の何倍か。
ただし、管口の位置を腹とする。
【参考】
・うなり。:https://tanakah17191928.blogspot.com/2023/06/blog-post_18.html
問4【気柱の共鳴】
図のように、閉管の管口の近くにスピーカーを置き、スピーカーから振動数$f_0$の音を出したところ、閉管内の気柱は基本振動で共鳴した。スピーカーから出る音の振動数を$f_0$から徐々に大きくしていったところ、まず振動数$f_1$で共鳴し、次に振動数$f_2$で共鳴した。
$f_2$は$f_1$の何倍か。
ただし、管口の位置を腹とする。
・閉管の長さを$L$とすると、$\lambda_1 = \dfrac{4}{3}L$
$f_1 = \dfrac{v}{\lambda_1} = \dfrac{3v}{4L}$
$\lambda_2 = \dfrac{4}{5}L$
$f_2 = \dfrac{v}{\lambda_2} = \dfrac{5v}{4L}$
$\dfrac{f_2}{f_1} = \dfrac{\dfrac{5v}{4L}}{\dfrac{3v}{4L}} = \dfrac{5}{3}$
・令和元年度第2回高認物理基礎過去問解説に戻る。
$f_1 = \dfrac{v}{\lambda_1} = \dfrac{3v}{4L}$
$\lambda_2 = \dfrac{4}{5}L$
$f_2 = \dfrac{v}{\lambda_2} = \dfrac{5v}{4L}$
$\dfrac{f_2}{f_1} = \dfrac{\dfrac{5v}{4L}}{\dfrac{3v}{4L}} = \dfrac{5}{3}$
・令和元年度第2回高認物理基礎過去問解説に戻る。