R3年度第2回高認物理基礎大問1解説
大問1
問1【時速と秒速】
速さ54km/hは何m/sか。また、この速さで1s間に進む距離は何mか。・$54 \times 1000 \div (60 \times 60) = \dfrac{54000}{3600} = \dfrac{540}{36} = 15$(m/s)
1s間に15m進む。
問2【相対速度】
東西方向の直線道路を自動車Aと自動車Bが走行している。自動車Aに対する自動車Bの相対速度は東向きに26m/sであった。
自動車Aの速度が西向きに12m/sであるとき、自動車Bの速度はいくらか。
・$v_{\mathrm{B}} - v_{\mathrm{A}} = 26$
$v_{\mathrm{A}} = -12$
$v_{\mathrm{B}} - (-12) = 26$
$v_{\mathrm{B}} + 12 = 26$
$v_{\mathrm{B}} = 26 - 12 = 14$
よって、東向きに14m/s
問3【速度と距離】
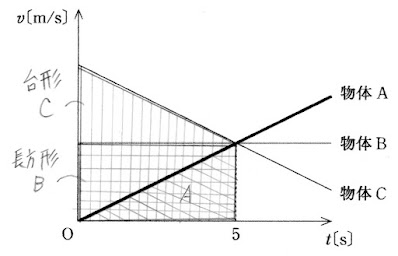
図は、$x$軸上を運動する3つの物体A、B、Cの速度$v$〔m/s〕と時刻$t$〔s〕の関係をそれぞれ表したものである。時刻$t = 0$sに3つの物体は$x$軸の原点Oに位置していた。
時刻$t = 5$sに、原点Oから最も離れた位置にある物体はどれか。
・物体Aが進んだ距離は図の三角形Aの面積であり、物体Bが進んだ距離は図の長方形Bの面積であり、物体Cが進んだ距離は図の台形Cの面積である。
台形C>長方形B>三角形A
よって、物体Cである。
最高点に達するのは、投射してから何s後か。
ただし、空気抵抗は無視できるものとし、重力加速度の大きさを$9.8 \mathrm{m/s^2}$とする。
・小球の速度$v = 19.6 - 9.8t$(m/s)は最高点で0になるので、$19.6 - 9.8t = 0$
$9.8t = 19.6$
$t = \dfrac{19.6}{9.8} = \dfrac{196}{98} = 2$(s)
【参考】
・H30年度第1回高認物理基礎大問1解説:https://tanakah17191928.blogspot.com/2023/06/h30_16.html
・令和3年度第2回高認物理基礎過去問解説に戻る。
台形C>長方形B>三角形A
よって、物体Cである。
問4【投げ上げ】
地面から小球を鉛直上向きに速さ19.6m/sで投射した。最高点に達するのは、投射してから何s後か。
ただし、空気抵抗は無視できるものとし、重力加速度の大きさを$9.8 \mathrm{m/s^2}$とする。
・小球の速度$v = 19.6 - 9.8t$(m/s)は最高点で0になるので、$19.6 - 9.8t = 0$
$9.8t = 19.6$
$t = \dfrac{19.6}{9.8} = \dfrac{196}{98} = 2$(s)
【参考】
・H30年度第1回高認物理基礎大問1解説:https://tanakah17191928.blogspot.com/2023/06/h30_16.html
・令和3年度第2回高認物理基礎過去問解説に戻る。